此為 Three.js 中物體的遠近關係 系列文章 - 第 3 篇：

1. Three.js 中物體的遠近關係 (1) - 什麼是深度測試？
2. Three.js 中物體的遠近關係 (2) - 左手/右手座標系與齊次座標
3. Three.js 中物體的遠近關係 (3) - 深度值的計算方式
4. Three.js 中物體的遠近關係 (4) - 對數深度值
5. Three.js 中物體的遠近關係 (5) - 渲染物體的順序

前言

上一篇提到了所有 像素(fragment) 對應的深度值都會落在 [0, 1] 區間內，0 代表這個 像素(fragment) 離相機最近，而 1 代表離相機最遠。但每個物體與相機之間的距離都不一樣，要如何把這些距離都轉換到深度值的 [0, 1] 區間內呢？這篇文章將討論如何將物體的距離($ z $ 值)轉換成 [0, 1] 區間內的深度值

深度值的線性轉換

要將所有物體的 $ z $ 值轉換到 [0, 1] 區間，最簡單的方式就是所謂的線性轉換：

$$ \large z_{depth} = \frac{z - \text{near}}{\text{far} - \text{near}} $$

套用以上方程式後

• 在 近平面 上的物體 $ z = near => z_{depth} = 0 $
• 在 遠平面 上的物體 $ z = far => z_{depth} = 1 $

假設 $ near = 1, far = 50 $ 可以畫出以下的圖，在 near 與 far 之間的所有 $ z $ 值，都轉換到了 [0, 1] 之間的深度值

實際上深度值的轉換函式

雖然上面線性轉換的方式可以把所有 $ z $ 值都轉換到 [0, 1] 的區間內，但實際上並不會使用這種簡單的線性轉換，原因是人的眼睛對於近處的物體比遠處的還要敏感，眼前的物體能很好的辨別他們之間的前後關係，至於越遠的物體在視野內會顯得越小就會更難分辨他們的前後關係。因此上面的線性方程不能很好的模擬人眼實際看起來的狀況，為了要模擬人眼這種近處分辨率高、遠處分辨率低的狀況，實際上深度值的轉換函式 $ z_{depth} $ 是和 $ 1/z $ 成正比的：

$$ \large z_{depth} = \frac{1/z - 1/near}{1/far - 1/near} $$

• 在 近平面 上的物體 $ z = near => z_{depth} = 0 $
• 在 遠平面 上的物體 $ z = far => z_{depth} = 1 $

以 $ z = 10 $ 來看，原本的線性函式大約只涵蓋了 [0, 0.2] 區間的範圍，而這個與 $ 1/z $ 成正比的函式則是涵蓋了約 [0, 0.9] 這麼廣的深度值範圍，這代表與 $ 1/z $ 成正比進行轉換的函式，對於近處的物體有更大範圍的深度值可以去覆蓋，也就是近處要比遠處更能分辨物體的前後關係

與 $ 1/z $ 成正比的轉換函式可以很好的將原本的 $ z $ 值轉換到深度值的 [0, 1] 區間，也符合實際上人眼的感知狀況，但為什麼用以上函式就可以很好的模擬人眼感知的狀況呢？下面我們打算用數學推導出這個與 $ 1/z $ 成正比的轉換函式

3D 投影到 2D

在進入正式的數學推導前我們需要了解一些關於投影的技巧，由於 3D 的物體最終要呈現在 2D 的電腦螢幕上，所以勢必有一個將 3D 座標投影到 2D 座標的技術，最常見的有 透視投影 (Perspective projection) 跟 正交投影 (Orthographic projection)

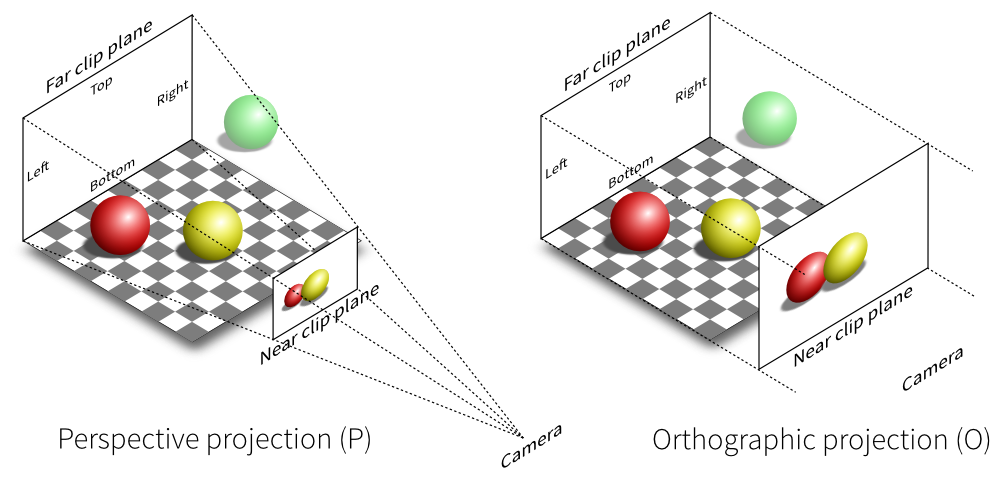
透視投影如下面左圖所示，以相機為原點，會定義一個 近平面 (Near plane) 與 遠平面 (Far plane)，在近平面與遠平面之中的這個類梯形區域有個專有名詞叫做 視錐體 (frustum)，在視錐體區域內的所有物體最終都會被投影到近平面上，如紅球跟黃球，而在視錐體區域外的物體會被排除，如綠球，稱之為 視錐體剔除 (Frustum Culling)，另外透視投影的一個特性是他就像人眼一樣，近處的物體看起來會較大、遠處物體看起來較小，因為黃球比較近、紅球比較遠，所以可以看到最後在 2D 近平面 上的投影，黃球比較大而紅球比較小，而右下圖的正交投影就沒有這個特性，即使黃球比紅球近，但正交投影到近平面上時，兩顆球的大小是一樣的

圖片來源

OpenGL 中的投影

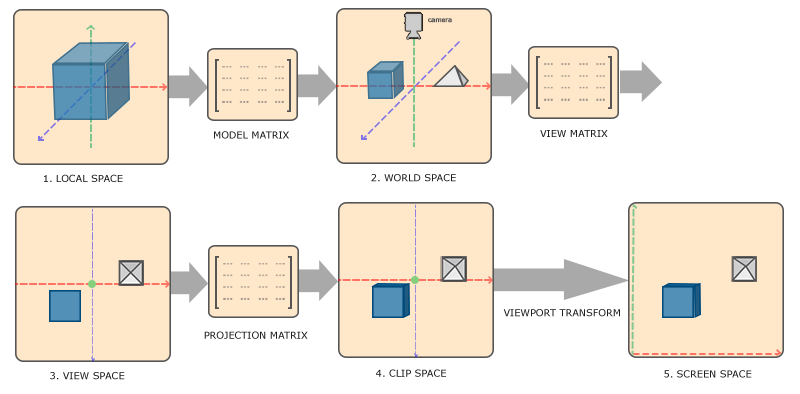
接著來看 Three.js 的底層 OpenGL 中是如何將 3D 的物體投影到 2D 的平面上，在 Vertex shader 做的事情 這篇文章中提過物體的頂點數據會轉換到不同的座標系統，從一開始的 本地座標 (local coordinate) 最後轉換到顯示在螢幕上的 螢幕座標 (screen coordinate) ，而投影這件事是將物體以相機為原點的 3D 座標系投影到 2D 近平面 上，而以相機為原點的座標系就是下圖中的 View space 觀察座標 (view coordinates)，觀察座標 (view coordinates) 會經過一個 投影矩陣 (projection matrix) 的計算進而變成 Clip space 裁剪座標 (clip coordinates)，這其實就是上面所說的將 3D 物體投影到 2D 平面的過程，而中間的數學計算是將 3D 物體所在的 觀察座標 (view coordinates) 乘以 投影矩陣 (projection matrix) 變成 2D 平面的 裁剪座標 (clip coordinates)

圖片來源

透視投影的過程

圖片來源

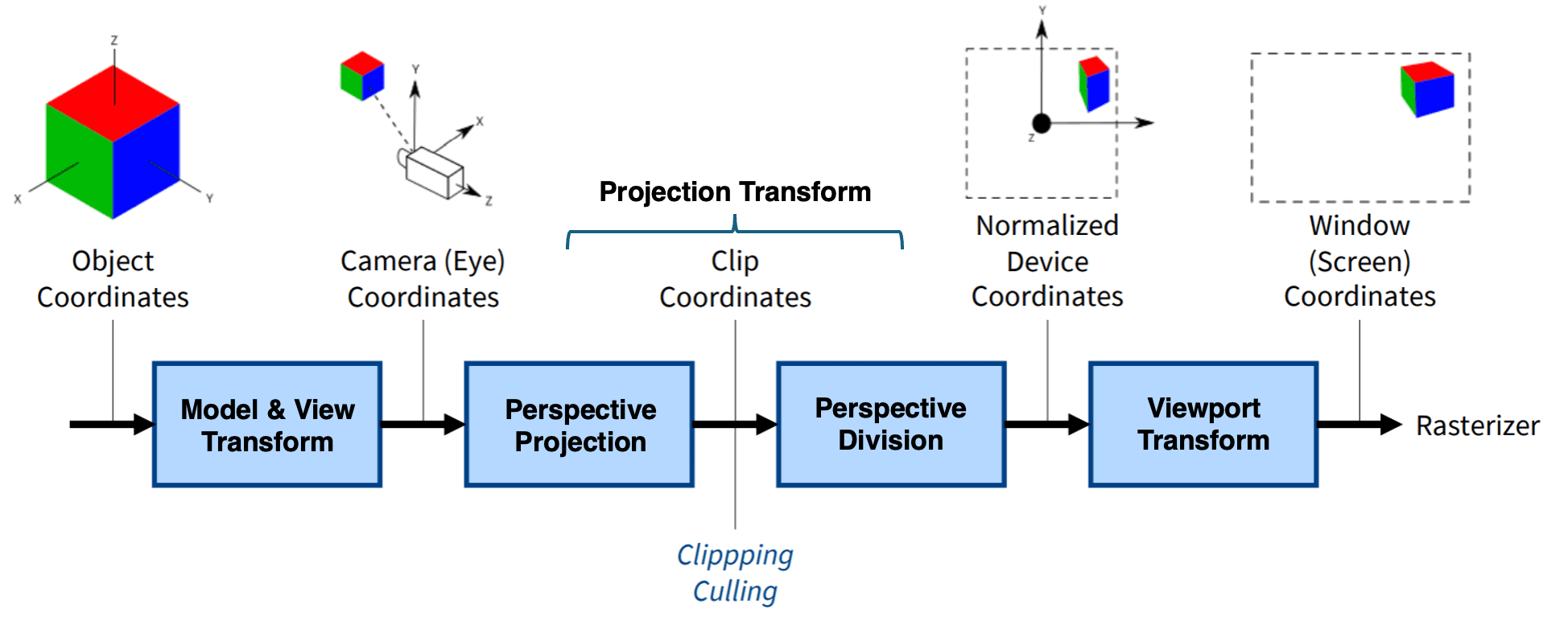
以下我們特別專注來看透視投影在 OpenGL 中是經由哪些過程，最終轉換為我們在電腦螢幕上看到的畫面：

1. 物體座標 (Object coordinates)

指的是以物體自身中心為原點的座標系，這對應到上圖中的 1. Local space

2. 相機座標 (Camera coordinates)

物體座標 經由 Model & View Transform (也就是乘以 Model matrix 及 View Matrix) 後，會轉換為相機座標，相機座標指的是以相機為原點的座標系，對應到的是上圖中的 3. View space

3. 裁剪座標 (Clip coordinates)

相機座標經過透視投影到近平面上後變成裁剪座標，上面提到的黃球因為離相機比較近、紅球比較遠，所以透視投影到裁剪座標後，黃球相較於紅球會看起來比較大，在這個階段也會執行一個叫做 裁剪踢除(Clipping culling) 的過程，跟上面所提的 視錐體剔除 (Frustum culling) 是一樣的意思，以上面例子來看就是指綠球在視錐體的區域外而無法投影到近平面上

4. 標準化設備座標 (Normalized Device Coordinates)

簡寫做 NDC，NDC 是物體最終呈現在畫面上的前一個座標系，目的是讓座標系限制在一個固定的區間，在 OpenGL 中 NDC 的座標被限制在 [-1, 1] 之間，在轉換為 NDC 座標前會經過一個叫做 透視除法 (Perspective division) 的過程，這個東西有點難用文字敘述，比較適合用數學來說明，所以我們將在下面的數學推導中提及

5. 螢幕座標 (Screen coordinates)

在得知螢幕寬高後就可以將 NDC 座標轉換為螢幕座標，NDC 座標中的 [-1, -1] 對應到螢幕的左下角、[0, 0] 對應到螢幕的中間、[1, 1] 對應到螢幕的右上角，這個轉換的過程稱之為視口變換(Viewport transform)，假設螢幕的寬高為 1440*900，那麼 NDC 座標的 [0, 0] 代表的就是螢幕座標的 [720, 450]

到目前為止我們講了許多關於透視投影的過程，為的就是讓大家在進入下面的數學推導時可以清楚了解各個座標是如何進行轉換的，接著就要開始數學推導了，以下藉由透視投影最終推導出深度值 $ Z_{depth} $ 與 $ 1/z $ 成正比的深度轉換函式

---

透視投影 (Perspective projection)

透視投影將 觀察座標 $ (x_e, y_e, z_e, w_e) $ 乘以一個的 $ 4x4 $ 投影矩陣 (projection matrix) 轉換成 裁剪座標 $ (x_p, y_p, z_p, w_p) $，接下來的目標是求出這個 $ 4x4 $ 的投影矩陣

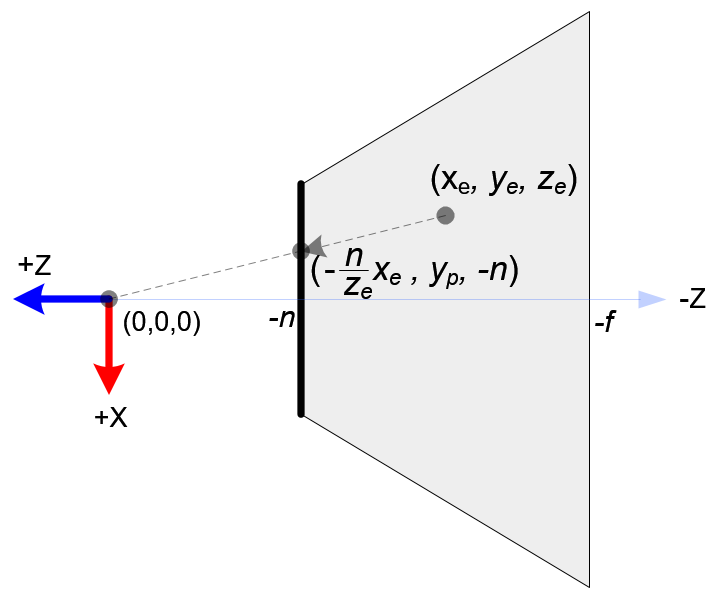
$$ \begin{bmatrix} x_p \\ y_p \\ z_p \\ w_p \end{bmatrix} = projection \; matrix \cdot \begin{bmatrix} x_e \\ y_e \\ z_e \\ w_e \end{bmatrix} $$

第一步我們先從 $ z $ 軸看起，轉換 $ z $ 軸座標很簡單，由於每個點最後都會投影到近平面上，所以 $ z $ 軸的座標值一律都會變成 $ -n $，也就是 $ z_p = -n $

P.S. $ -n $ 指的是近平面所在的 $ z $ 軸數值，請看 NDC 座標圖片 的左圖

下一步讓我們來推導 $ x $ 及 $ y $ 軸投射到近平面上的座標，從下面左圖 $ x, z $ 軸的剖面可知 觀察座標 $ (x_e, y_e, z_e) $ 投影到近平面的 裁剪座標 $ (x_p, y_p, z_p) $ 時會形成兩個直角三角形，而我們可以利用直角三角形邊長成比例的關係得到：

$$
\displaystyle
\frac{x_p}{x_e} = \frac{z_p}{z_e} \quad \Rightarrow \quad x_p = \frac{-n}{z_e} \times x_e \tag{1}
$$

同理右圖以 $ y, z $ 軸的剖面可得：

$$
\displaystyle
\frac{y_p}{y_e} = \frac{z_p}{z_e} \quad \Rightarrow \quad y_p = \frac{-n}{z_e} \times y_e \tag{2}
$$

圖片來源

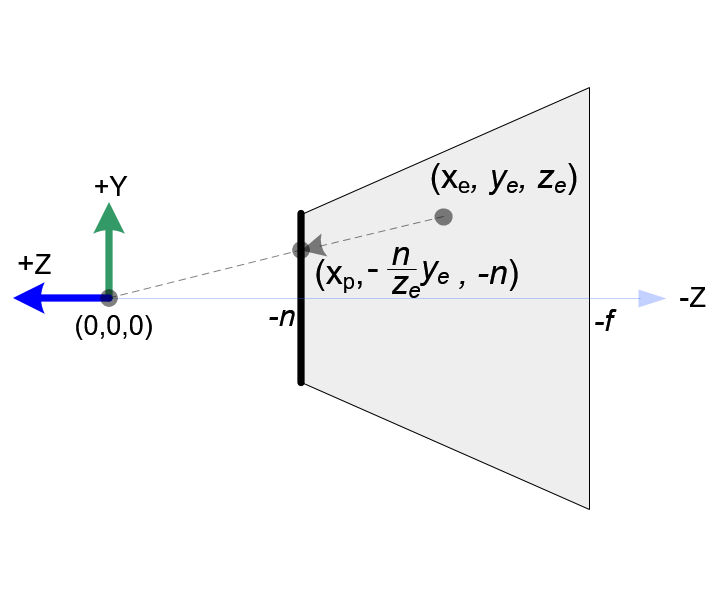
透視除法 (Perspective division)

還記得我們上一篇系列文中提到的齊次矩陣嗎？裁剪座標 $ (x_p, y_p, z_p) $ 的齊次座標表示為 $ (x_p, y_p, z_p, w_p) $，而將齊次座標轉換回三維座標時會將每個維度都除以 $ w_p $，這就是透視除法的含義

從上面直角三角形邊長成比例的推導我們發現 $ x_p $ 與 $ y_p $ 都除以 $ -z_e $，根據透視除法會將每個維度都除以 $ w_p $ 的定義，我們可以讓 $ w_p = -z_e $ 於是首先求出投影矩陣第四列的數值

$$ \begin{bmatrix} x_p \\ y_p \\ z_p \\ w_p \end{bmatrix} = \begin{bmatrix} . & . & . & . \\ . & . & . & . \\ . & . & . & . \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} x_e \\ y_e \\ z_e \\ w_e \end{bmatrix} $$

標準化設備座標 (Normalized Device Coordinates)

執行完 透視除法 (Perspective division) 的下一步就是將座標轉換為 NDC，在 OpenGL 中 NDC 的範圍被定義在 [-1.0, 1.0] 之間

這裡我們以 $ l, r, t, b, n, f $ 分別代表左、右、上、下、近平面、遠平面的座標數值，如此一來從裁剪座標轉換到 NDC 所做的映射為：

• x 軸： $ [l, r] \Rightarrow [-1, 1] $
• y 軸： $ [b, t] \Rightarrow [-1, 1] $
• z 軸： $ [n, f] \Rightarrow [-1, 1] $

這裡需要特別注意的是，裁剪座標是右手座標系而 NDC 是左手座標系，下圖可以很明顯的看出來 $ z $ 軸的數值是相反的

NDC 座標圖片

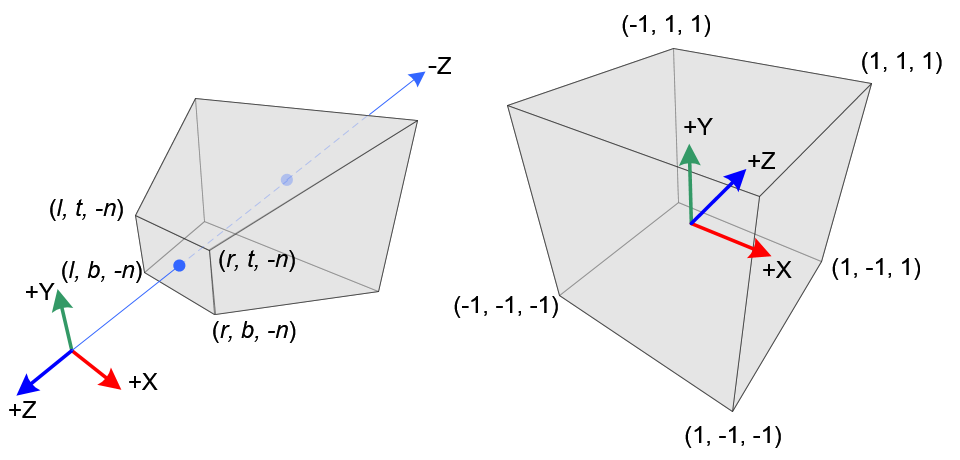
NDC 座標轉換

下面我們藉由 NDC 座標範圍被定義在 [-1.0, 1.0] 之間，嘗試求出投影矩陣中第一及第二列的數值

計算 $ x_{ndc} $

由於 $ x_p $ 會映射到 NDC 座標的 -1 到 1 之間，這裡我們採用線性轉換的方式計算 $ x_{ndc} $

$$
\displaystyle
x_{ndc} = \frac{1 - (-1)}{r - l} x_p + \beta
$$

將 $ (x_p, x_{ndc}) $ 分別帶入 $ (r, 1) $ 進去：

$$
\displaystyle
1 = \frac{2r}{r - l} + \beta
$$

接著求出 $ \beta $：

$$
\displaystyle
\beta = 1 - \frac{2r}{r - l} = \frac{r - l}{r - l} - \frac{2r}{r - l} = \frac{-l - r}{r - l} = -\frac{r + l}{r - l}
$$

所以我們得出：

$$
\displaystyle
x_{ndc} = \frac{2x_p}{r - l} - \frac{r + l}{r - l}
$$

將 $ x_p $ 套入 $ (1) $ 式計算的結果：

$$ \begin{align*} x_{ndc} &= \frac{\displaystyle 2 \cdot \frac{n x_e}{-z_e}}{r - l} - \frac{r + l}{r - l} \\ &= \frac{2n \cdot x_e}{(r - l)(-z_e)} - \frac{r + l}{r - l} \\ &= \frac{\displaystyle \frac{2n}{r-l} \cdot x_e}{-z_e} + \frac{\displaystyle \frac{r+l}{r-l} \cdot z_e}{-z_e} \\ &= \left( \underbrace{\frac{2n}{r-l} \cdot x_e + \frac{r+l}{r-l} \cdot z_e}_{\displaystyle x_p} \right) \cdot \frac{1}{-z_e} \end{align*} $$

至此我們推導出投影矩陣的第一列了

$$ \begin{bmatrix} x_p \\ y_p \\ z_p \\ w_p \end{bmatrix} = \begin{bmatrix} \displaystyle \frac{2n}{r-l} & 0 & \displaystyle \frac{r+l}{r-l} & 0 \\ . & . & . & . \\ . & . & . & . \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} x_e \\ y_e \\ z_e \\ w_e \end{bmatrix} $$

計算 $ y_{ndc} $

將 $ y_{ndc} $ 也套用上面計算 $ x_{ndc} $ 一樣的方式

$$
\displaystyle
y_{ndc} = \frac{1 - (-1)}{t - b} y_p + \beta
$$

將 $ (y_p, y_{ndc}) $ 分別帶入 $ (t, 1) $ 進去：

$$
\displaystyle
1 = \frac{2t}{t - b} + \beta
$$

求出 $ \beta $：

$$
\displaystyle
\beta = 1 - \frac{2t}{t - b} = \frac{t - b}{t - b} - \frac{2t}{t - b} = \frac{-b - t}{t - b} = -\frac{t + b}{t - b}
$$

所以我們得出：

$$
\displaystyle
y_{ndc} = \frac{2y_p}{t - b} - \frac{t + b}{t - b}
$$

將 $ y_p $ 套入 $ (2) $ 式計算的結果：

$$ \begin{align*} x_{ndc} &= \frac{\displaystyle 2 \cdot \frac{n y_e}{-z_e}}{t - b} - \frac{t + b}{t - b} \\ &= \frac{2n \cdot y_e}{(t - b)(-z_e)} - \frac{t + b}{t - b} \\ &= \frac{\displaystyle \frac{2n}{t-b} \cdot y_e}{-z_e} + \frac{\displaystyle \frac{t+b}{t-b} \cdot z_e}{-z_e} \\ &= \left( \underbrace{\frac{2n}{t-b} \cdot y_e + \frac{t+b}{t-b} \cdot z_e}_{\displaystyle y_p} \right) \cdot \frac{1}{-z_e} \end{align*} $$

於是我們也推導出投影矩陣的第二列

$$ \begin{bmatrix} x_p \\ y_p \\ z_p \\ w_p \end{bmatrix} = \begin{bmatrix} \displaystyle \frac{2n}{r-l} & 0 & \displaystyle \frac{r+l}{r-l} & 0 \\ 0 & \displaystyle \frac{2n}{t-b} & \displaystyle \frac{t+b}{t-b} & 0 \\ . & . & . & . \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} x_e \\ y_e \\ z_e \\ w_e \end{bmatrix} $$

計算 $ z_{ndc} $

最後來求投影矩陣第三列的數值，因為 $ z_p $ 是觀察座標投影到近平面上的 $ z $ 值，這代表他的數值跟原本的 $ x_e, y_e $ 都沒有關係，所以我們可以設 $ z_p = A \cdot z_e + B \cdot w_e $，於是投影矩陣變成

$$ \begin{bmatrix} x_p \\ y_p \\ z_p \\ w_p \end{bmatrix} = \begin{bmatrix} \displaystyle \frac{2n}{r-l} & 0 & \displaystyle \frac{r+l}{r-l} & 0 \\ 0 & \displaystyle \frac{2n}{t-b} & \displaystyle \frac{t+b}{t-b} & 0 \\ 0 & 0 & A & B \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} x_e \\ y_e \\ z_e \\ w_e \end{bmatrix} $$

另外根據 $ z $ 軸 NDC 座標的定義：

$$
\displaystyle
z_{ndc} = \frac{z_p}{w_p} = \frac{Az_e + Bw_e}{-z_e}
$$

在觀察空間 $ w_e = 1 $ 所以：

$$
\displaystyle
z_{ndc} = \frac{z_p}{w_p} = \frac{Az_e + B}{-z_e} \tag{3}
$$

接著將 $ (z_e, z_{ndc}) $ 帶入 $ (-n, -1) $ 進去：

$$
\displaystyle
\frac{-An+B}{n} = -1 \Rightarrow -An+B = -n
$$

於是可以求出 $ B $：

$$
\displaystyle
B = An - n
$$

同樣的將 $ (z_e, z_{ndc}) $ 帶入 $ (-f, 1) $ 進去：

$$
\displaystyle
\frac{-Af+B}{f} = 1 \Rightarrow -Af+B = f \Rightarrow -Af + (An - n) = f \Rightarrow -(f-n)A = f+n
$$

可以求出 $ A $：

$$
\displaystyle
A = -\frac{f+n}{f-n}
$$

接著我們把 $ A $ 的數值帶回去以求出 B：

$$
\begin{align*}
B = -\frac{f + n}{f - n} n -n \
= -\left( 1 + \frac{f + n}{f - n} \right) n \
= -\frac{f - n + f + n}{f - n} n \
= -\frac{2 f n}{f - n}
\end{align*}
$$

好不容易終於把投影矩陣都求出來了！

$$ \begin{bmatrix} x_p \\ y_p \\ z_p \\ w_p \end{bmatrix} = \begin{bmatrix} \displaystyle \frac{2n}{r-l} & 0 & \displaystyle \frac{r+l}{r-l} & 0 \\ 0 & \displaystyle \frac{2n}{t-b} & \displaystyle \frac{t+b}{t-b} & 0 \\ 0 & 0 & \displaystyle -\frac{f+n}{f-n} & \displaystyle -\frac{2 f n}{f - n} \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} x_e \\ y_e \\ z_e \\ w_e \end{bmatrix} $$

深度測試的 z 值

我們如此辛苦的推導出透視投影的投影矩陣，目的是想知道深度測試中的深度值是怎麼被算出來的，以下我們用 $ z_{depth} $ 表示深度值

根據定義，$ z $ 軸 NDC 座標 ($ z_{ndc} $)的範圍在 [-1, 1] 之間，而深度值 ($ z_{depth} $) 範圍在 [0, 1] 之間，所以我們會將 $ z_{ndc} $ 從 [-1, 1] 轉換到 [0, 1] 之間以表示 $ z_{depth} $

$$
z_{depth} = \frac{z_{ndc} + 1}{2}
$$

根據 $ (3) $ 式 $ z_{ndc} $ 等於：

$$ \begin{align*} \displaystyle z_{ndc} &= \frac{Az_e + B}{-z_e} = \frac{\displaystyle -\frac{f+n}{f-n}z_e - \frac{2 f n}{f - n}}{-z_e} = \displaystyle \frac{f+n}{f-n} + \frac{2fn}{(f - n)z_e} \end{align*} $$

於是 $ z_{depth} $ 等於：

$$ \begin{align*} \displaystyle z_{depth} &= \frac{\displaystyle \frac{f+n}{f-n} + \frac{2fn}{(f - n)z_e} + 1}{2} \\ &= \frac{\displaystyle \frac{f+n}{f-n} + \frac{2fn}{(f - n)z_e} + \frac{f-n}{f-n}}{2} \\ &= \frac{\displaystyle \frac{2f}{f-n} + \frac{2fn}{(f - n)z_e}}{2} \\ &= \frac{\displaystyle f + \frac{fn}{z_e}}{f-n} \\ \end{align*} $$

共同除以 $ f \cdot n $：

$$ \begin{align*} \displaystyle z_{depth} &= \frac{\displaystyle \frac{1}{n} + \frac{1}{z_e}}{\displaystyle \frac{1}{n}-\frac{1}{f}} = \frac{\displaystyle - \frac{1}{z_e} -\frac{1}{n}}{\displaystyle \frac{1}{f}-\frac{1}{n}} \end{align*} $$

分子的 $ \displaystyle z_e $ 位於右手座標系的觀察座標，也就是說近平面及遠平面的座標是 $ (-n, -f) $，如果我們希望改為左手座標系表示，也就是以 $ (n, f) $ 代表近平面及遠平面，z 軸的正負號會被反轉，所以最終 $ z_{depth} $ 會等於：

$$ \begin{align*} \displaystyle z_{depth} &= \frac{\displaystyle \frac{1}{z} -\frac{1}{n}}{\displaystyle \frac{1}{f}-\frac{1}{n}} \end{align*} $$

這就是一開始提到 實際上深度值的轉換函式 了，深度值與 $ 1/z $ 成正比的關係

總結

一開始我們打算讓深度值做最簡單的線性轉換，但這種轉換方式不符合人眼的看東西的狀況，接著我們學習了 3D 投影到 2D 的方式 - 透視投影 跟 正交投影，以及學習 OpenGL 中透視投影經過了哪些座標系的轉換過程，最終我們藉由透視投影中的數學將觀察座標轉換成裁剪座標的過程中證明透視投影的深度值 $ z_{depth} $ 是與 $ 1/z $ 成正比的關係

參考資料

Projection Matrix - 數學推導的主要參考文章
深度测试
OpenGL Tutorial 14 - Depth Buffer
Transformation matrix for projection of 3D objects into a 2D plane (projection transform)
一看就懂的 OpenGL ES 教程——走进 3D 的世界之坐标系统（下篇）
OpenGL 的归一化设备坐标系明明是左手坐标系，为什么其他教程上都说 OpenGL 是右手坐标系？